NBA Betting: Using Team Statistics to Classify the Spread. Can I make a Profit?


All analyses done using Python.

Background

Machine learning has increasingly been used in the sporting world, transforming the tactics and strategies of teams. However along with the impact of big data and machine learning on sports directly, there has been an increasing interest in machine learning related to sports prediction and betting, especially in the National Basketball Association (NBA). Much of the work thus far has focused on predicting the outcome of games. While interesting, this isn't necessarily useful, as betting agencies often do not provide betting options in regards to who wins or loses games.

Thus as a big basketball fan I wanted to see if I could take public NBA data and use it to make money betting on the spread.

The Point Spread

The point spread can be thought of as the betting world's term for "margin of victory". Betting sites will frequently place a predicted point spread for a matchup between two teams playing an NBA game. The idea behind the predicted spread is for bettors to bet on if this point spread will be exceeded or not in the particular game.


Image Source


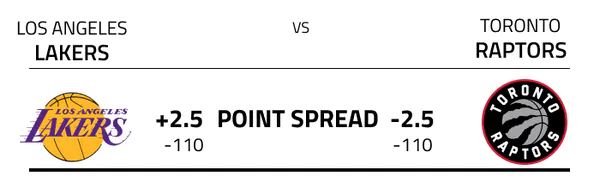
The caveat is that based on the performance of the teams up to that point in the season, betting sites will typically label one team as the favorite to win the game, and the other team as the underdog. In the image above, the Toronto Raptors are considered the favorite team to win the matchup, as denoted by the negative point spread (2.5). Notably, point spreads are often set at a decimal value so that actual margins of victory will never equal the predicted point spread, which would complicate the betting outcome.

If the outcome of this game were to result in the Toronto Raptors winning by 3 points or more, the outcome of the game would be that the Raptors (the favorite) beat the spread. If the Los Angeles Lakers either win the game, or lose by less than 3 points, the Lakers (the underdog) beat the spread. Thus a bettor can place a bet each game on whether they believe the favorite team will win by more than the predicted spread (margin of victory), or the underdog will either win the game or lose and keep the game closer than expected (lose by less than the predicted spread).

Data Collection

Basketball Statistics

The basketball statistics used for this analysis involved the team-level performance averaged throughout the season in which the game was played. The team level performance data was representative of the teams productivity, relative to the productivity of their opponents they allow each game.

As a specific example, the Utah Jazz (see image below) outscore their opponents by an average of 9.2 points per game during the 2020-21 NBA season. Similarly, they on average attempted 3.2 less field goals than their opponents, and rebounded 5.6 times more per game.


Image Source

Thus for each NBA team, differential statistics for each season between 2010 and 2021 were collected and scraped from the ESPN website using the pandas read_html library. Data for each season were extracted from the website and placed into separate pandas dataframes and subsequently joined into a single dataframe containing yearly team statistics for each NBA team over each season.

Game Outcomes and Betting Data

Basketball game scores and betting information was downloaded in the form of csv files from the Online Sportsbook Directory (NBA Scores and Odds Archives), a resource for historical betting data. The game data provided included the date, teams playing, location, and points scored. Betting information included the predicted favorite team to win, the predicted point spread, as well as the “money lines” which are used to calculate the payout of a winning bet.

Data Preparation

Joining the Data

The dataframe containing game outcomes were merged with the basketball statistics dataframe by identifying the date of play and the teams involved, as no two teams would play each other twice in the same day. Because the data provided information about where the games were played, an additional column was created with a binary value to indicate if the favorite team was playing in their home arena or not.

The dataframe was subsequently adjusted dropping unnecessary columns for analysis, such as team names and game dates, and split into the feature set and label set. The resulting feature set contained only numerical columns related to the seasonal average game statistics for the favorite teams and underdog teams, the predicted spread, in addition to a binary feature indicating whether the home team was playing at home or away.


Cleaning the Data

Because the team differential statistics for each season were only representative of regular season games, all playoff games in the dataset were removed from the data.

Further, as one of our features included whether or not the favorite team was playing in their home arena, a portion of the games from the 2019-2020 season were removed from the data. These games were played at a neutral site in Florida with no fans due to the COVID-19 pandemic.


Feature Selection

My dataset up to this point included 38 features, many of which I considered to be unimportant to the outcome variable. Because of this I decided to use the Lasso Regression to select a subset of the features which may be more directly associated with my target outcome.

As my classification decision was based on the difference between the predicted and actual spread (2 continuous variables), I decided to use the difference between the two as my target variable for the Lasso Regression.

After the analysis, I found that only 9 of the original 38 features were considerably associated with the difference between the predicted and actual spread, and therefore chose to keep them in my subsequent analyses:

(Favorite/Underdog) indicates whether the statistic is relative to the favorite or underdog team for the specific feature.

Labeling the Outcome Variable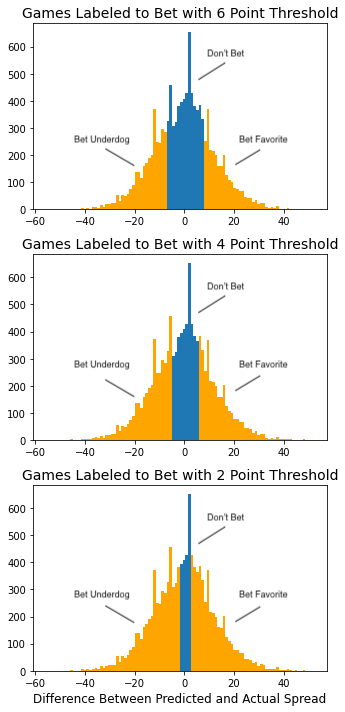

Due to the nature of the data I knew I would have 3 different classes for my outcome variable. The next task was to determine how I wanted to label the data. When should I decide to bet or not? And if I am to bet, should I bet on the favorite or on the underdog to beat the spread?

Here it is very important to understand how the difference between the predicted and actual spread is calculated. In the example at the top of the page, the Toronto Raptors are predicted to win the game by 2.5 points. In this example, if the Toronto Raptors were to win the game by 10 points, the difference between the predicted and actual spread would be 7.5 points, as the favorite won by an additional 7.5 points more than the predicted spread. On the flip side, if the Lakers were to win by 2 points, the difference between the predicted and actual spread would be -4.5 points (they were predicted to lose by 2.5 points, and they won by 2 points, a 4.5 point swing in the opposite direction).

Here I chose to create a parameter which I could tune to alter how I labeled the data. The figure to the right illustrates this parameter, and three of the different thresholds I used when labeling my data. In the figures, all games which occur to the right of zero are games in which the favorite beat the spread, whereas games to the left are games in which the underdog beat the spread. Therefore, for games which resulted in an actual spread X points or more away from the predicted spread, I labeled them to bet for the underdog or favorite to beat the spread, depending on the direction of the difference. Using this method I could create a way to tune how aggressive or conservative I'd prefer my models to be when predicting bets.


Histograms showing the distribution of games with respect to the difference between the predicted and actual spread. The orange represent the games with actual spreads greater than X points away from the predicted spreads.

Preparing for Analysis

Now that I had collected, cleaned and labeled my data, I split my data into training and testing sets using the sklearn train_test_split function, with a test size of 0.25 and a fixed random state.

Subsequently, I transformed all numeric variables using the sklearn StandardScalar function to set the means equal to zero as well as standardize the variance.

Algorithms - Fitting and Tuning

Model Selection and Tuning

The models I chose to use for this classification problem were Logistic Regression, Random Forest, and Support Vector Classifier. Each model was tested on the data using each of the spread difference thresholds (0.5, 2, 4, and 6 points).

For each of the thresholds, the Logistic Regression and SVC were fit to the data with their default parameters. Following the initial fitting of the models, I used cross validation in conjunction with the sklearn RandomizedSearchCV and GridSearchCV functions to tune the models and minimize overfitting. The Random Forest Models were intially fit using RandomizedSearchCV to determine the most appropriate parameters for the data. Because the optimization was conducted for each threshold, the optimal parameters may differ between algorithms at different thresholds (for example the optimal max depth for the Random Forest at threshold 0.5 may differ from the optimal max depth at threshold 6).

For the rest of this post, the initial default models will be referred to by their model name, while the models which were optimized will be referred to as [Model Name] - Optimal.

Results

In total, I implemented 20 different models. Five algorithms, each fit at the four spread difference thresholds. The summary of model outputs is presented in Table 1 at the end of this section, providing the accuracy, recall, precision, and F1 scores on both the training and test set.

For each game that my model labeled I should bet on I placed a $10 bet. Of the 20 models, ten made a profit, although the profits were negligible. It is important to note that when evaluating the financial gain, not only is the success rate of the bet important, but the frequency the model bets is important as well. Some models were particularly accurate when choosing to bet, however did not bet frequently enough to make a considerable amount of money, while others were very poor at betting correctly, but did not bet frequently, minimizing the financial losses. Therefore, I will discuss the results in terms of both total profit as well as average profit per game bet.

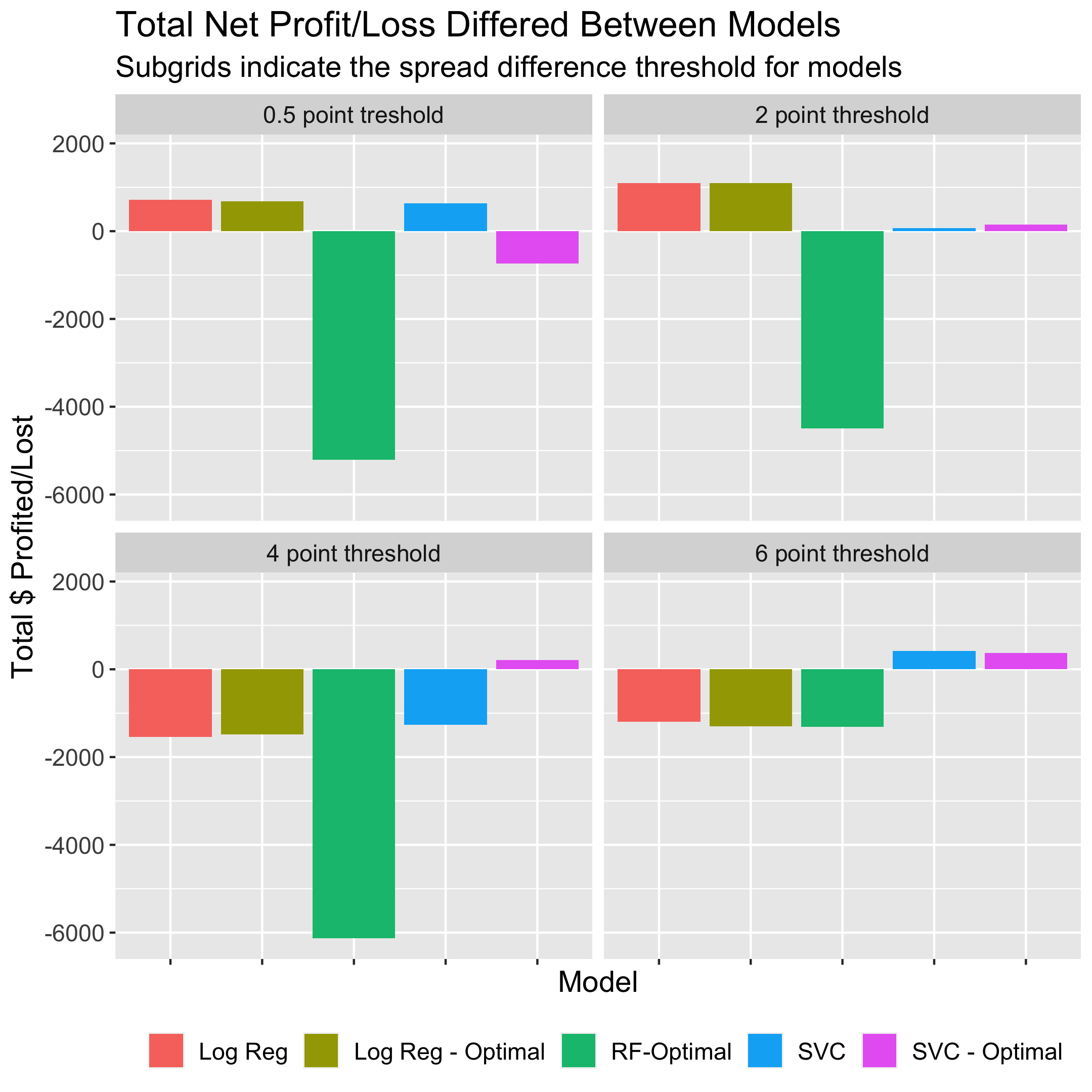
Total Profit

The models with the total highest payout were the logistic regression (both the default and optimal at the 2 point threshold) which netted $1,090, which at face value appears significant. However the $1,090 was made after betting on 2,666 games (100% of games in the test set). The next two models with the highest payout were also the default and optimal logistic regression models at the 0.5 point threshold, netting $719 and $684 respectively after betting on 100% of the games.

The Random Forest - Optimal at the 2, 0.5, and 4 point thresholds were the least succesful models in terms of net gain, losing $4490, $4212, and $6126 respectively. Not only were the models bad at betting, but the reason they lost so much money is that they bet on 100%, 100%, and 99.9% of the games in the test set, respectively. I found it particularly interesting that the Random Forest models with optimal parameters performed so poorly. The figure below illustrates the total net profit achieved from each model.

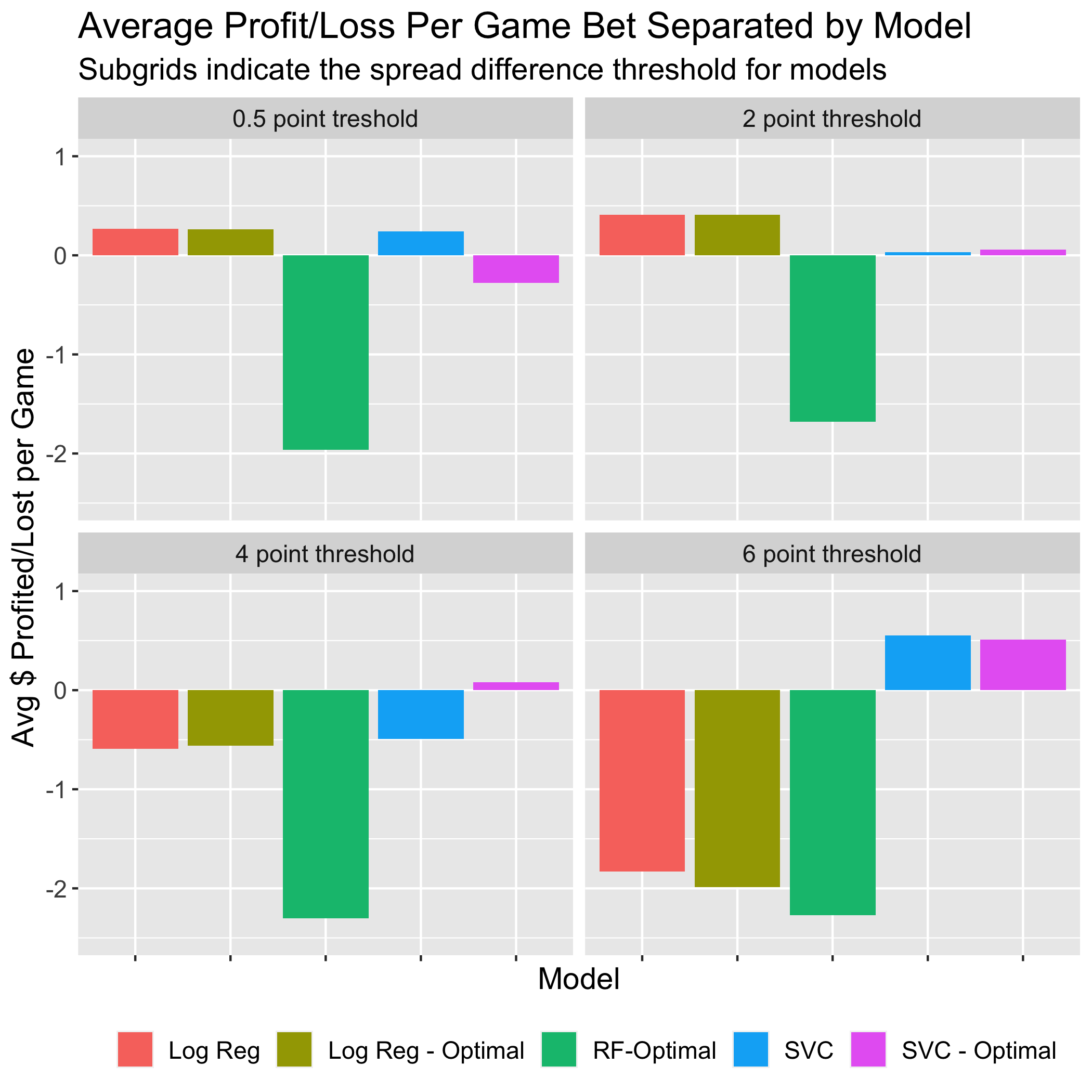
Average Profit per Game Bet

The Support Vector Classifiers (both default and optimal at the 6 point threshold) were the most successful models in terms of average gain per bet. The reason they did not profit the most however is due to the conservative betting of the models, betting on only 28.5% and 27% of the games, respectively. Following these two the next most successful models were the logistic regression (both the default and optimal at the 2 point threshold) which gained an average of 41 cents per game bet, while also betting on 100% of the games.

On the other hand, the Random Forest - Optimal (4 and 6 point threshold) were the least successful models losing an average of $2.30 and $2.27 per game bet. The difference between these models however lied in the fact that the Random Forest at the 4 point threshold bet 99.9% of the time while the Random Forest at the 6 point threshold bet only 21.6% of the time. After these two models the next most poorly performing model was the Logistic Regression - Optimal, losing $1.99 per game bet, betting 24.4% of the time. The figure below illustrates the average net profit achieved from each model.



Table 1. Model summaries grouped by threshold. Profitable models are highlighted in green.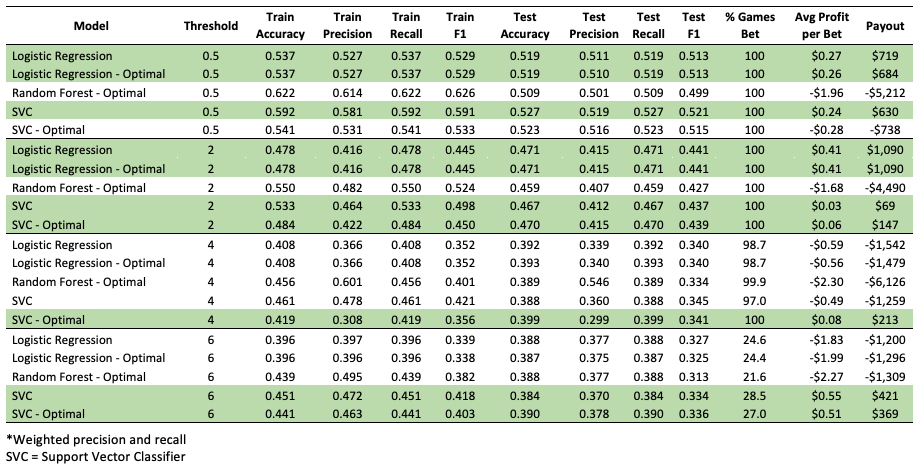


Closing

While I'm disappointed that my models weren't very succesful at making money, it doesn't surprise me that basic team level statistics can't provide the necessary information to accurately predict the spread outcome. The outcomes of individual games can be largely influenced by factors that can't be captured in the data of a team's season-long average performance. These factors could include player injuries, the amount of rest teams have, as well as in-season player trades that can considerably alter a team's performance.

Continuing this work, I'll look into other sources and types of data that may be more applicable in betting situations. There are plenty of APIs available that allow access to an enormous amount of NBA data (including injuries and the number of days rest teams are getting between games).

I can't forget that there are also a number of other betting opportunities. For instance, betting agencies often provide an estimate of the total points scored in an NBA game. Bettors can bet whether or not they believe the total score will exceed the estimate. At first glance, I'd think that using the direct offensive statistics (instead of team differentials) could be useful in predicting this outcome. As I continue my work on this project that is something I will absolutely explore.